Содержание
Тема № 1. Предмет и метод статистики
История, пути и направления статистической науки
Предмет статистики
Отрасли статистики
Метод статистики
Закон больших чисел
Статистическая закономерность
Задачи статистики
Организация государственной статистики в РФ
Ряды распределения
Тема № 2. Статистическое наблюдение
Понятие статистического наблюдения
Формы статистического наблюдения
Виды статистического наблюдения
Виды несплошного наблюдения
Способы статистического наблюдения
Программно-методологические вопросы статистического наблюдения
Тема № 3. Сводка и группировка
Статистическая сводка
Статистическая группировка
Виды группировок
Система группировок
Тема № 4. Статистические таблицы
Понятие статистической таблицы
Виды таблиц в зависимости от разработки подлежащего
Виды таблиц по характеру сказуемого
Элементы таблицы
Запись цифр в таблицах
Тема № 5. Абсолютные и относительные величины
Абсолютные статистические величины
Относительные статистические величины
Виды относительных величин
Тема № 6. Графический метод
Понятие графика
Схема статистических графиков по форме графического способа
Схема статистических графиков по способу и задачам построения
Основные правила построения графиков
Тема № 7. Средние величины
Сущность и задачи средних величин
Расчет средней
Средняя арифметическая
Способ моментов
Средняя гармоническая
Общая из индивидуальных средних
Степенные средние
Структурные средние
Тема № 8. Показатели вариации
Необходимость расчета показателей вариации
Абсолютные показатели вариации
Относительные показатели вариации
Дисперсия альтернативного признака
Виды дисперсий и правила их сложения
Эмпирическое корреляционное отношение (ЭКО)
Некоторые математические свойства дисперсий
Тема № 9. Экономические индексы
Понятие индексов
Индивидуальные индексы
Сводные индексы
Средние индексы
Цепные и базисные индексы с постоянными и переменными весами
Индексы постоянного состава, переменного состава и структурных сдвигов
Индексы Пааше, Ласпейреса и "идеальный индекс" Фишера
Территориальные индексы
Индексы планового задания и выполнения плана
Тема № 10. Ряды динамики
Задачи статистики в области рядов динамики
Понятие и виды рядов динамики
Несопоставимость уровней рядов динамики
Показатели изменения уровней ряда
Средние характеристики ряда динамики
Выявление основной тенденции развития динамических рядов
Прогнозирование и интерполяция
Тема № 11. Статистическое измерение связи
Задачи статистики в изучении связи.
Взаимосвязанные признаки и их классификация.
Виды и формы связей, различаемые в статистике.
Методы изучения связей
Тема № 12. Выборочный метод
Основы выборочного метода
Ошибки выборки
Средняя ошибка выборки
Предельная ошибка выборки
Основные виды выборки, способы отбора
Примеры задач
Численность выборки
Повторный групповой отбор
Многоступенчатый отбор
Бесповторный отбор
Определение границ изменения генеральной средней
Предмет и метод статистики
История, пути и направления статистической науки
Термин "статистика" появился в середине 18 века. Означал "государствоведение". Получил распространение в монастырях. Постепенно приобрел собирательное значение.
С одной стороны, статистика – это совокупность числовых показателей, характеризующих общественные явления и процессы (статистика труда, статистика транспорта) .
С другой – под статистикой понимается практическая деятельность по сбору, обработке, анализу данных по различным направлениям общественной жизни.
С третьей стороны, статистика – это итоги массового учета, опубликованные в различных сборниках.
Наконец, в естественных науках статистикой называются методы и способы оценки соответствия данных массового наблюдения математическим формулам.
Таким образом, статистика – это общественная наука, изучающая количественную сторону массовых общественных явлений в неразрывной связи с их качественной стороной.
Ученые, внесшие вклад в развитие статистики
Предмет статистики
Статистика изучает количественно определенные качества массовых социально-экономических явлений.
Существует несколько точек зрения на статистику как на науку:
Явления общественной жизни – это сложное сочетание различных элементов.
Размеры и соотношения количества и качества отдельных явлений статистика выражает при помощи определенных понятий, статистических показателей. Числовое значение показателя, относящееся к определенному месту и времени, называют величиной показателя.
Отрасли статистики
Общая теория статистики – это лишь фундамент. В любой своей части она связана с другими науками.
|
Общая теория статистики |
||||||||||||
|
Демографическая статистика |
Экономическая статистика |
Статистика образования |
Медицинская статистика |
Спортивная статистика |
||||||||
|
Статистика труда |
Статистика заработной платы |
Статистика мат. -техн. снабжения |
Статистика транспорта |
Статистика связи |
Статистика финансового кредита |
|||||||
|
Высшие финансовые вычисления |
Статистика денежного обращения |
Статистика валютных курсов |
Прочие |
|||||||||
Статистика также разрабатывает теорию наблюдения.
Метод статистики
Метод статистики предполагает следующую последовательность действий:
Прохождение каждой стадии связано с использованием специальных методов, объясняемых содержанием выполняемой работы.
Закон больших чисел
Массовый характер общественных законов и своеобразие их действий предопределяет необходимость исследования совокупных данных.
Закон больших чисел порожден особыми свойствами массовых явлений. Последние в силу своей индивидуальности, с одной стороны, отличаются друг от друга, а с другой – имеют нечто общее, обусловленное их принадлежностью к определенному классу, виду. Причем единичные явления в большей степени подвержены воздействию случайных факторов, нежели их совокупность.
Закон больших чисел в наиболее простой форме гласит, что количественные закономерности массовых явлений отчетливо проявляются лишь в достаточно большом их числе.
Таким образом, сущность его заключается в том, что в числах, получающихся в результате массового наблюдения, выступают определенные правильности, которые не могут быть обнаружены в небольшом числе фактов.
Закон больших чисел выражает диалектику случайного и необходимого. В результате взаимопогашения случайных отклонений средние величины, исчисленные для величины одного и того же вида, становятся типичными, отражающими действия постоянных и существенных фактов в данных условиях места и времени.
Тенденции и закономерности, вскрытые с помощью закона больших чисел, имеют силу лишь как массовые тенденции, но не как законы для каждого отдельного случая.
Статистическая закономерность
Статистические закономерности изучают распределение единиц статистического множества по отдельным признакам под воздействием всей совокупности факторов.
Статистическая закономерность выступает как объективная закономерность сложного массового процесса и является формой причинной связи. Она обнаруживается в итоге массового статистического наблюдения. Этим обуславливается ее связь с законом больших чисел.
Статистическая закономерность с определенной вероятностью гарантирует устойчивость средних величин при сохранении постоянного комплекса условий, порождающих данное явление.
Задачи статистики
Организация государственной статистики в РФ
Принципы:
Система государственной статистики имеет иерархическую структуру. Эта структура имеет федеральный, республиканский, краевой, областной, окружной, городской и районный уровни.
Госкомстат имеет управления, отделы, вычислительный центр.
Ряды распределения
Рядами распределения называются группировки особого вида, при которых по каждому признаку, группе признаков или классу признаков известны численность единиц в группе либо удельный вес этой численности в общем итоге.
Ряды распределения могут быть построены или по количественному, или по атрибутивному признаку.
Ряды распределения, построенные по количественному признаку, называются вариационными рядами. Ряд распределения может быть построен по непрерывно варьирующему признаку (когда признак может принимать любые значения в рамках какого-либо интервала) и по дискретно варьирующему признаку (принимает строго определенные целочисленные значения) .
Непрерывно варьирующий признак изображается графически при помощи гистограммы. Дискретный же ряд распределения графически представляется в виде полигона распределения.
Статистическое наблюдение
Понятие статистического наблюдения
Статистическое наблюдение – это сбор необходимых данных по явлениям, процессам общественной жизни. Но это не всякий сбор данных, а лишь планомерный, научно организованный, систематический и направленный на регистрацию признаков, характерных для исследуемых явлений и процессов. От качества данных, полученных на первом этапе, зависят конечные результаты исследования.
Формы статистического наблюдения
Различают две основные формы статистического наблюдения – отчетность и специально организованное наблюдение.
Отчетность – это такая форма наблюдения, при которой предприятия, организации представляют в статистические и вышестоящие органы постоянные сведения, характеризующие их деятельность. Отчетность предоставляется по заранее определенной программе в строго определенные сроки и содержит важнейшие показатели, необходимые в процессе ежедневной работы.
Специально организованное наблюдение – такое наблюдение, которое организуется со специальной целью на определенную дату для получения данных, которые в силу различных причин не собираются статистической отчетности, а также с целью проверки данных статистической отчетности.
Виды статистического наблюдения
По времени регистрации фактов статистическое наблюдение может быть непрерывным, периодическим и единовременным.
Непрерывное (текущее) наблюдение – ведется систематически (т.е. регистрация фактов производится по мере их свершения) . Пример – ЗАГС.
Периодическое наблюдение – повторяется через определенные равные промежутки времени. Пример – перепись населения.
Единовременное наблюдение – производится по мере надобности без соблюдения определенной периодичности. Пример – оценка и переоценка основных фондов.
По охвату единиц совокупности выделяют сплошное и несплошное наблюдение.
Сплошным называется наблюдение, при котором исследованию подвергаются все единицы изучаемой совокупности.
Несплошным называется такое наблюдение, при котором исследованию подвергается только часть единиц изучаемой совокупности, отобранная определенным образом.
Виды несплошного наблюдения
Исследуются какие-то осредненные показатели и распространяются на всю совокупность.
Исследуются наиболее крупные единицы изучаемого явления.
Его основой является случайный отбор. Результат гарантируется с определенной вероятностью р.
Подвергаются тщательному исследованию отдельные единицы совокупности, обычно представители новых типов, либо самые лучшие (худшие) единицы. Результаты переносятся на всю совокупность. Позволяет выявить тенденции.
Способы статистического наблюдения
Основанием для регистрации фактов могут служить либо документы, либо высказанное мнение, либо хронометражные данные. В связи с этим различают наблюдение:
В статистике применяются следующие способы сбора информации:
Программно-методологические вопросы статистического наблюдения
Каждое наблюдение проводится с конкретной целью. При его проведении необходимо установить, что подлежит обследованию. Надо решить следующие вопросы: Объект наблюдения – совокупность предметов, явлений, у которых должны быть собраны сведения. При определении объекта указываются его основные отличительные черты (признаки) . Всякий объект массовых наблюдений состоит их отдельных единиц, поэтому надо решить вопрос о том, каков тот элемент совокупности, который послужит единицей наблюдения.
Единица наблюдения – это составной элемент объекта, который является носителем признаков, подлежащих регистрации и основой счета.
Ценз – это определенные количественные ограничения для объекта наблюдения.
Признак – это свойство, которое характеризует определенные черты и особенности, присущие единицам изучаемой совокупности.
Программа наблюдения – это перечень признаков, подлежащих регистрации. Программа находит отражение в формуляре наблюдения. Выделяются организационные вопросы: перечень мероприятий, обеспечивающих правильность наблюдения, а также оргплан, где учитываются органы наблюдения, время наблюдения, порядок приема и сдачи материала, порядок получения информации.
Период наблюдения – время, в течение которого должна быть осуществлена регистрация.
Критическая дата наблюдения – дата, по состоянию на которую сообщаются сведения.
Критический момент – момент времени, по состоянию на который производится регистрация наблюденных фактов.
Сводка и группировка
Статистическая сводка
Статистическая сводка – это операция по обработке собранных данных, которые выражаются в виде показателей, относящихся к каждой единице объекта статистического наблюдения. В результате сводки эти данные превращаются в систему статистических таблиц и промежуточных итогов. По результатам сводки можно выявить наиболее типичные черты и закономерности изучаемых явлений.
Предварительно составляется программа и план сводки.
В программе определяется подлежащее и сказуемое сводки. Подлежащее составляет вся совокупность группы или части, на которые разбивается совокупность. Сказуемое – это те показатели, которые характеризуют каждую группу, часть или всю совокупность в целом.
План сводки – содержит организационные вопросы.
Статистическая группировка
Статистическая группировка – это метод исследования массовых общественных явлений путем выделения и ограничения однородных групп, через которые раскрываются существенные черты и особенности состояния и развития всей совокупности.
Основные задачи, которые решаются с помощью группировок:
Важнейшие проблемы:
Группировочный признак – это признак, по которому происходит определение единиц в группе. Его выбор зависит от цели группировки и существа данного явления.
Число групп определяется с таким расчетом, чтобы в каждую группу попало достаточно большое число единиц.
Интервалы могут быть равными и неравными. Последние в свою очередь делятся на равномерно возрастающие и равномерно убывающие.
Виды группировок
(1) Типологические группировки
Их задача – выявление социально-экономических типов или однородных в существенном отношении групп.
|
№ п/п |
Социально-экономические типы |
Мужчины |
Женщины |
||
|
1980 |
1992 |
1980 |
1992 |
||
|
1. |
Работники |
– |
– |
– |
– |
|
2. |
Крестьяне |
– |
– |
– |
– |
|
3. |
Служащие |
– |
– |
– |
– |
(2) Структурные группировки
Их задача – изучение состава отдельных типических групп при помощи объединения единиц совокупности, близких друг к другу по величине группировочного признака.
|
№ п/п |
Количество посадочных мест |
Количество столов |
Число занятых |
Товарооборот на 1 место |
|
1. |
до 25 |
– |
– |
– |
|
2. |
16 – 50 |
– |
– |
– |
|
3. |
51 – 70 |
– |
– |
– |
|
4. |
71 – 100 |
– |
– |
– |
(3) Аналитические группировки
Их задача – выявления влияния одних признаков на другие (выявить связь между социально-экономическими явлениями) .
|
№ п/п |
Группы магазинов по числу рабочих мест |
Число магазинов |
Товарооборот |
|
|
на 1 работника |
на 1 раб. место |
|||
|
1. |
до 5 |
100 |
12,0 |
13,0 |
|
2. |
6 – 10 |
50 |
14,0 |
16,0 |
|
3. |
11 – 15 |
10 |
15,0 |
17,0 |
|
4. |
16 – 20 |
4 |
30,0 |
39,0 |
|
5. |
21 – 25 |
2 |
31,0 |
42,0 |
(4) Комбинационные группировки
В них производится разделение совокупности на группы по двум или более признакам. При этом группы, образованные по одному признаку, разбиваются на подгруппы по другому признаку.
Такие группировки дают возможность изучить структуру совокупности по нескольким признакам одновременно.
|
№ п/п |
Группы предприятий по объему основных фондов |
Оплата труда в рублях |
Пол |
Количество единиц |
|
1. |
до 200 |
100 – 120 |
М |
– |
|
Ж |
– |
|||
|
120 – 140 |
М |
– |
||
|
Ж |
– |
|||
|
140 – 160 |
М |
– |
||
|
Ж |
– |
|||
|
2. |
200 – 400 |
100 – 120 |
М |
– |
|
Ж |
– |
|||
|
120 – 140 |
М |
– |
||
|
Ж |
– |
|||
|
140 – 160 |
М |
– |
||
|
Ж |
– |
|||
|
3. |
400 – 600 |
100 – 120 |
М |
– |
|
Ж |
– |
|||
|
120 – 140 |
М |
– |
||
|
Ж |
– |
|||
|
140 – 160 |
М |
– |
||
|
Ж |
– |
|||
|
4. |
600 – 800 |
100 – 120 |
М |
– |
|
Ж |
– |
|||
|
120 – 140 |
М |
– |
||
|
Ж |
– |
|||
|
140 – 160 |
М |
– |
||
|
Ж |
– |
Система группировок
Социально-экономический анализ предполагает использование системы простых и комбинационных группировок.
Также очень часто прибегают к вторичной группировке – перегруппировка уже сгруппированных данных. Вторичная группировка может быть проведена методом простого укрупнения интервала.
Часто также используется процентная перегруппировка.
Пример: Группировка фермерских хозяйств по наличию скота.
Исходные данные:
|
№ п/п |
Группы хозяйств по числу голов |
% фермерских хозяйств |
% поголовья |
% по всему кол-ву скота |
|
1. |
без голов |
26,4 |
2,8 |
9,9 |
|
2. |
с 1-й головой |
20,3 |
9,5 |
8,9 |
|
3. |
с 2-мя головами |
14,6 |
11,8 |
11,1 |
|
4. |
с 3-мя –– " –– |
9,3 |
10,5 |
9,8 |
|
5. |
с 4-мя –– " –– |
8,3 |
12,1 |
11,2 |
|
6. |
с 5-ю –– " –– |
21,1 |
53,3 |
56,1 |
|
|
Всего: |
100 |
100 |
100 |
Процентная перегруппировка
|
№ п/п |
Группы хозяйств по уровню развития |
% фермерских хозяйств |
% поголовья |
% по всему кол-ву скота |
|
1. |
Низкий |
50 |
14,9 |
21,3 |
|
2. |
Средний |
30 |
34,6 |
32,5 |
|
3. |
Высокий |
20 |
50,5 |
53,2 |
|
|
Всего: |
100 |
100 |
100 |
Расчеты:
Статистические таблицы
Понятие статистической таблицы
Статистическая таблица – это наиболее рациональная форма изложения и изображения статистической сводки. Таблица состоит из пересечения граф и строк.
Таблица – это статистическое предложение, которое имеет подлежащее и сказуемое.
Подлежащее таблицы – показывает, о чем идет речь в таблице.
Сказуемое таблицы – показывает, какими признаками характеризуется подлежащее.
Виды таблиц в зависимости от разработки подлежащего
В ней дается перечисление единиц совокупности.
В подлежащем дается не перечень единиц совокупности, а их группы.
Ее познавательная сторона заключается в том, что появляется возможность проследить влияние на признаки сказуемого не одного, а двух и более факторов, т.е. признаков, которые легли в основание комбинированной группировки или в подлежащее комбинационной таблицы. Каждая из групп, на которые разбивается подлежащее, в свою очередь разбивается на подгруппы.
Виды таблиц по характеру сказуемого
Такая разработка, в которой мы используем лишь 1-2 отдельно взятых признака.
Используется комбинация признаков.
Элементы таблицы
Запись цифр в таблицах
Если одно из числовых выражений данного признака равно нулю, то пересечение соответствующей графы и строки перечеркивается.
Если числовые значения признака неизвестны, то в пересечении графы и строки ставится многоточие.
Если пересечение графы и строки не имеет смысла, то ставится "Х".
Если в таблице проценты по отношению к какому-либо предыдущему году, то этот год должен быть показан в таблице, несмотря на указание его в заголовке.
Абсолютные и относительные величины
Абсолютные статистические величины Абсолютные статистические величины показывают объем, размеры, уровни различных социально-экономических явлений и процессов. Они отражают уровни в физических мерах объема, веса и т.п. В общем абсолютные статистические величины – это именованные числа. Они всегда имеют определенную размерность и единицы измерения. Последние определяют сущность абсолютной величины.
Типы абсолютных величин
Виды абсолютных величин
Абсолютные величины отражают наличие тех или иных ресурсов, это основа материального учета. Они наиболее объективно отражают развитие экономики.
Абсолютные величины являются основой для расчета разных относительных статистических показателей.
Относительные статистические величины
Относительные статистические величины выражают количественные соотношения между явлениями общественной жизни, они получаются в результате деления одной абсолютной величины на другую.
Знаменатель (основание сравнения, база) – это величина, с которой производится сравнение.
Сравниваемая (отчетная, текущая) величина – это величина, которая сравнивается.
Относительная величина показывает, во сколько раз сравниваемая величина больше или меньше базисной или какую долю первая составляет по отношению ко второй. В ряде случае относительная величина показывает, сколько единиц одной величины приходится на единицу другой.
Важное свойство – относительная величина абстрагирует различия абсолютных величин и позволяет сравнивать такие явления, абсолютные размеры которых непосредственно несопоставимы.
Форма выражения относительных величин
В результате сопоставления одноименных абсолютных величин получают неименованные относительные величины. Они могут выражаться в виде долей, кратных соотношений, процентных соотношений, в виде промилле и т.д.
Результатом сопоставления разноименных величин являются именованные относительные величины. Их название образуется сочетанием сравниваемой и базисной абсолютных величин.
Выбор формы зависит от характера аналитической задачи, которая состоит в том, чтобы с наибольшей ясностью выразить соотношение.
Виды относительных величин
Все применяемые на практике относительные статистические величины подразделяются на следующие виды.
Относительная величина динамики Достигнутый показатель / базисный показатель. Относительная величина планового задания Плановый показатель / базисный показатель. Относительная величина выполнения плана Достигнутый показатель / плановый показатель. Относительная величина структуры Отношение частей и целого.
Относительная величина координации
Соотношение частей целого между собой.
Относительная величина интенсивности Характеризует распределение явления в определенной среде (насыщенность каким-либо явлением) . Это всегда соотношение разноименных величин.
Относительная величина уровня социально-экономического явления Характеризует размеры производства различных видов продукции на душу населения.
Относительная величина сравнения
Представляет собой отношение одноименных величин, относящихся к различным объектам.
Графический метод
Понятие графика
Графики – это средства обобщения статистической информации. Графический метод – особая знаковая система, знаковый язык.
Графики в статистике имеют не только иллюстративное значение, они позволяют получить дополнительные знания о предмете исследования, которые в цифровом варианте остаются скрытыми, невыявленными. Любое статистическое исследование на основе какого-либо метода в конечном итоге дополняется использованием графического метода.

Схема статистических графиков по форме графического способа
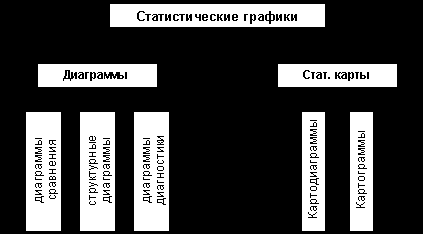
Схема статистических графиков по способу и задачам построения Основные правила построения графиков Каждый график должен содержать следующие основные элементы:
Средние величины Сущность и задачи средних величин Средняя величина – это обобщающая количественная характеристика совокупности однотипных явлений по одному варьирующему признаку.
Она отражает объективный уровень, достигнутый в процессе развития явления к определенному моменту или периоду.
Средняя представляет значение определенного признака в совокупности одним числом и элиминирует индивидуальные различия значений отдельных величин совокупности.
Необходимость сочетается со случайностью, поэтому средние величины связаны с Законом больших чисел. Суть этой связи в том, что при осреднении случайные отклонения индивидуальных величин от средней погашаются, а в средней отчетливо выявляется основная тенденция развития.
Важнейшая особенность средней величины – в том, что она относится к единице изучаемой совокупности и через характеристику единицы характеризует всю совокупность в целом.
Основные свойства средней величины:
Средние позволяют исключить влияние индивидуальных значений признака, т.е. они являются абстрактными величинами. Поэтому средние должны употребляться на основе сгруппированных данных.
Расчет средней К расчету средней предъявляются два основных требования:
Одинаковые по форме и технике вычисления средние в одних случаях могут быть огульными, а в других – общими в зависимости от того, с какой целью они интерпретируются.
Говоря о методологии исчисления средних, не надо забывать, что средняя всегда дает обобщенную характеристику лишь по одному признаку. Каждая же единица совокупности имеет много признаков. Поэтому необходимо рассчитывать систему средних, чтобы охарактеризовать явление со всех сторон.
Расчет средних величин производится по правилам, которые разрабатываются математической статистикой. Задача ОТС – дать смысловую, преимущественно экономическую интерпретацию результатам расчетов, произведенных по формулам.
Признак, по которому производится осреднение, называется осредняемым признаком –. Величина осредняемого признака у каждой единицы совокупности называется ее индивидуальным значением.
Значение признака, которое встречается у групп единиц или у отдельных единиц и не повторяется, называется вариантом признака – Средняя величина этих вариантов, или просто средняя, обозначается.
Средняя арифметическая
Простая средняя арифметическая для ряда данных рассчитывается по формуле: Но можно также рассчитать среднюю арифметическую взвешенную как: Свойства средней арифметической:
Способ моментов
Часто мы сталкиваемся с расчетом средней арифметической упрощенным способом. В этом случае используются свойства средней величины. Метод упрощенного расчета называется способом моментов, либо способом отсчета от условного нуля.
Способ моментов предполагает следующие действия:
|
|
|
|
|
|
|
|
до 70 |
65 |
15 |
-30 |
-3 |
-45 |
|
70-80 |
75 |
17 |
-20 |
-2 |
-34 |
|
80-90 |
85 |
13 |
-10 |
-1 |
-13 |
|
90-100 |
95 |
22 |
0 |
0 |
0 |
|
100-110 |
105 |
8 |
10 |
1 |
8 |
|
110-120 |
115 |
12 |
20 |
2 |
24 |
|
120-130 |
125 |
6 |
30 |
3 |
18 |
|
130-140 |
135 |
5 |
40 |
4 |
20 |
|
140 и более |
145 |
2 |
50 |
5 |
10 |
|
Сумма |
|
100 |
|
|
-12 |
Средняя гармоническая
Расчет средней гармонической связан с двумя причинами:
Расчет простой средней гармонической: Расчет средней гармонической взвешенной: Такой расчет имеет определенные трудности, которые заключаются в том, что не всегда ясно можно трактовать условие поставленной задачи. Поэтому перед тем, как приступать к расчету средней, необходимо разобраться в экономическом смысле данных, которыми вы располагаете.
|
Базисный |
Отчетный |
||
|
Фонд з/п |
Среднеспис. з/п |
Среднеспис. з/п |
Среднеспис. численность |
|
xf |
х |
x |
f |
|
Средняя гармоническая |
Средняя арифметическая |
||
Общая из индивидуальных средних
Рассчитывается по следующей формуле:
Степенные средние
Те средние величины, которые мы записали, относятся к степенным средним. В наиболее общем виде степенная средняя записывается следующим образом: В зависимости от k и образуются разные виды средних.
|
Степень k |
Вид средней |
Формула расчета |
|
k = 1 |
Арифметическая |
|
|
k = 2 |
Квадратическая |
|
|
k = 0 |
Геометрическая |
|
|
k = -1 |
Гармоническая |
|
Правило мажорантности:
Структурные средние
Величина средней определяется всеми значениями признака, встречающимися в данном ряду распределения. Различают такие структурные средние, как:
Мода
Это значение признака, которое встречается в ряду распределения чаще, чем другие его значения.
В дискретном ряду распределения значения моды определяются визуально. Если же ряд распределения задан как интервальный, то значение моды рассчитывается по следующей формуле:
Медиана
Это центральное значение признака, им обладает центральный член ранжированного ряда.
Прежде всего определяется порядковый номер медианы по формуле и строят ряд накопленных частот. Накопленной частоте, которая равна порядковому номеру медианы или первая его превышает, в дискретном вариационном ряду соответствует значение медианы, а в интервальном – медианный интервал.
Для интервального ряда медиана рассчитывается по следующей формуле:
Квартиль
Первый квартиль вычисляется по формуле:
Аналогично рассчитывается третий квартиль. Второй же квартиль равен медиане.
Дециль
Рассчитывается по аналогии с расчетом квартиля. Можно найти девять децилей.
Средняя должна исчисляться не просто тогда, когда есть вариация признака, а тогда, когда мы располагаем качественно однородным вариационным рядом. Среднюю как обобщающую характеристику нельзя применять к таким совокупностям, отдельные части которых подчиняются различным законам распределения (или) развития в отношении величины распределяемого признака.
Показатели вариации
Необходимость расчета показателей вариации Средняя представляет собой обобщающую статистическую характеристику, в которой получает количественное выражение типичный уровень признака, которым обладают члены изучаемой совокупности. Но одной средней нельзя отобразить все характерные черты статистического распределения. Возможны случаи совпадения средних арифметических при разном характере распределения.
Показатели вариации используются для характеристики и упорядочения статистических совокупностей.
Абсолютные показатели вариации
Для измерения размера вариации используются следующие абсолютные показатели: размах, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение.
Размах
Величина его целиком зависит от случайности распределения крайних членов ряда, и значение подавляющего большинства членов ряда не учитывается, в то время как вариация связана с каждым значением члена ряда.
Такие показатели, которые представляют собой средние, полученные из отклонений индивидуальных значений признака от их средней величины, лишены этого недостатка.
Между индивидуальными отклонениями от средней и колеблемостью конкретного признака существует прямая зависимость. Чем сильнее колеблемость, тем больше абсолютные размеры отклонений от средней.
Дисперсия
Среднее линейное отклонение
Среднее квадратическое отклонение
Дисперсию можно подсчитать и по следующей формуле: По этой формуле ленче считать дисперсию, когда имеешь дело с дискретным рядом распределения.
|
Годовой удой от одной коровы |
Середина интервала |
Число коров |
|
|
|
|
|
|
до 2-х |
1,5 |
40 |
6 |
-1,3 |
5,2 |
1,69 |
6,76 |
|
2-3 |
2,5 |
20 |
5 |
-0,3 |
0,6 |
0,09 |
0,18 |
|
3-4 |
3,5 |
20 |
7 |
+0,7 |
1,4 |
0,49 |
, 98 |
|
4-5 |
4,5 |
10 |
4,5 |
+1,7 |
1,7 |
2,89 |
2,89 |
|
5 и более |
5,5 |
10 |
5,5 |
+2,7 |
2,7 |
7,29 |
7,29 |
|
Сумма |
|
|
28 |
|
11,6 |
|
18,1 |
Относительные показатели вариации
Коэффициент осцилляции – Коэффициент относительного линейного отклонения – Коэффициент вариации– Дисперсия альтернативного признака Альтернативный признак – это такой признак, которым одни члены обладают, а другие – нет.
доля единиц, не обладающих признаком
доля единиц, обладающих признаком
Виды дисперсий и правила их сложения
Межгрупповая дисперсия
Между отдельными видами дисперсий существует взаимосвязь, которую можно записать в виде правила сложения дисперсий: Пример: Распределение сотрудников КБ по производительности труда 1. Расчет общей дисперсии
|
x |
f |
xf |
x 2 |
x 2 f |
|
10 |
50 |
50 |
100 |
500 |
|
11 |
150 |
165 |
121 |
1815 |
|
13 |
50 |
65 |
169 |
845 |
|
15 |
50 |
75 |
225 |
1125 |
|
18 |
70 |
126 |
324 |
2268 |
|
20 |
30 |
60 |
400 |
1200 |
|
|
40 |
541 |
|
7753 |
2. Расчет дисперсии по первой группе
|
x |
f |
xf |
x 2 |
x 2 f |
|
10 |
50 |
50 |
100 |
500 |
|
11 |
150 |
165 |
121 |
1815 |
|
13 |
50 |
65 |
169 |
845 |
|
|
25 |
280 |
|
3160 |
3. Расчет дисперсии по второй группе
|
x |
f |
xf |
x 2 |
x 2 f |
|
15 |
50 |
75 |
225 |
1125 |
|
18 |
70 |
126 |
324 |
2268 |
|
20 |
30 |
60 |
400 |
1200 |
|
|
15 |
261 |
|
4593 |
4. Расчет межгрупповой дисперсии
|
|
|
|
|
|
|
11,2 |
25 |
-2,325 |
5,405 |
135,140 |
|
17,4 |
15 |
3,875 |
15,015 |
225,234 |
|
|
40 |
|
|
360,375 |
5. Расчет средней из индивидуальных дисперсий Эмпирическое корреляционное отношение (ЭКО) На основании правила сложения дисперсий вычисляется эмпирическое корреляционное отношение (ЭКО) , которое равно квадратному корню из отношения межгрупповой дисперсии к общей:
Такой порядок вычисления обусловлен разложением общей вариации на вариацию, зависящую от фактора, положенного в основу группировки (в нашем примере – повышение и неповышение квалификации) , которая численно равна межгрупповой дисперсии, и общую вариацию.
Межгрупповая дисперсия составляет часть общей дисперсии и складывается под влиянием только одного группировочного фактора. Именно поэтому подкоренное выражение показывает долю вариации за счет группировочного признака.
ЭКО изменяется в переделах от нуля до единицы. Чем ближе его значение к единице, тем большая доля вариации падает на группировочный признак.
Некоторые математические свойства дисперсий
На основании свойств дисперсии ее можно подсчитать способом отсчета от условного нуля и способом моментов.
|
Интервал |
|
|
|
|
|
|
|
|
|
90-100 |
95 |
2 |
190 |
-30 |
-3 |
-6 |
9 |
18 |
|
100-110 |
105 |
6 |
630 |
-20 |
-2 |
-12 |
4 |
24 |
|
110-120 |
115 |
8 |
920 |
-10 |
-1 |
-8 |
1 |
8 |
|
120-130 |
125 |
18 |
2 250 |
0 |
0 |
0 |
0 |
0 |
|
130-140 |
135 |
5 |
675 |
10 |
1 |
5 |
1 |
5 |
|
140-150 |
145 |
4 |
580 |
20 |
2 |
8 |
4 |
16 |
|
150-160 |
155 |
3 |
465 |
30 |
3 |
9 |
9 |
27 |
|
160-170 |
165 |
2 |
330 |
40 |
4 |
8 |
16 |
32 |
|
170-180 |
175 |
2 |
350 |
50 |
5 |
10 |
25 |
50 |
|
|
|
50 |
6 390 |
|
|
14 |
|
180 |
Экономические индексы Понятие индексов В статистике под индексом понимается относительная величина (показатель) , выражающая изменение сложного экономического явления во времени, в пространстве или по сравнению с планом. В связи с этим различают динамические, территориальные индексы, а также индексы выполнения плана.
Многие общественные явления состоят из непосредственно несопоставимых явлений, поэтому основной вопрос – это вопрос сопоставимости сравниваемых явлений.
К какому бы экономическому явлению ни относились индексы, чтобы рассчитать их, необходимо сравнивать различные уровни, которые относятся либо к различным периодам времени, либо к плановому заданию, либо к различным территориям. В связи с этим различают базисный период (период, к которому относится величина, подвергаемая сравнению) и отчетный период (период, к которому относится сравниваемая величина) . При исчислении важно правильно выбрать период, принимаемый за базу сравнения.
Индексы могут относиться либо к отдельным элементам сложного экономического явления, либо ко всему явлению в целом.
Индивидуальные индексы Показатели, характеризующие изменение более или менее однородных объектов, входящих в состав сложного явления, называются индивидуальными индексами – i x .
Индекс получает название по названию индексируемой величины.
В большинстве случаев в числителе стоит текущий уровень, а в знаменателе – базисный уровень. Исключением является индекс покупательной способности рубля.
Индексы измеряются либо в виде процентов (%) , либо в виде коэффициентов.
Сводные индексы
Сложные явления, для которых рассчитывается сводный индекс, отличаются той особенностью, что элементы, их составляющие, неоднородны и, как правило, несоизмеримы друг с другом. Поэтому сопоставление простых сумм этих элементов невозможно. Сопоставимость может быть достигнута различными способами:
Цель теории индексов – изучение способов получения относительных величин, используемых для расчета общего изменения ряда разнородных явлений.
|
Товар |
Базисный |
Отчетный |
|
1 |
|
|
|
2 |
|
|
|
... |
|
|
|
n |
|
|
|
|
|
|
Индекс стоимости товарооборота Индекс цены товарооборота Индекс физического объема товарооборота Проблема выбора весов Если индексируемой величиной является качественный признак, то вес принимается на уровне текущего периода.
Если же индексируемой величиной является количественный признак, то вес принимается на уровне базисного периода.
Такой выбор весов позволяет записать следующую связь: Сводные индексы в агрегатной форме позволяют нам измерить не только относительное изменение отдельных элементов изучаемого явления и явления в целом в текущем периоде по сравнению с базисным, но и абсолютное изменение.
Например, если мы вычтем из числителя индекса цены его знаменатель, то мы получим абсолютное изменение стоимости товарооборота в результате изменения цен: То же самое можно сделать для индекса физического объема и для индекса товарооборота.
Средние индексы
Агрегатная форма индекса – одна из важнейших, но не единственная. В практических расчетах очень часто используются средние индексы. Это связано с тем, что, например, в индексе цены пересчет продукции, реализованной в текущем периоде, в базисные цены практически очень сложен. В то время как индивидуальные индексы цены на практике разрабатываются постоянно.
Агрегатный индекс цены тождественен среднему гармоническому индексу цены.
Агрегатный индекс физического объема тождественен среднему арифметическому индексу физического объема.
Проблема связана лишь с прочтением условия задачи.
Цепные и базисные индексы с постоянными и переменными весами Цепные индексы: Сумма произведений индивидуальных цепных индексов дает базисный индекс за соответствующий период.
Базисные индексы:
Увидим, что частное от деления последующего базисного индекса на предыдущий индекс дает нам цепной индекс за соответствующий период.
С постоянными весам
Цепные
Базисные
Преимущество сводных индексов с постоянными весами состоит в том, что их можно сравнивать между собой, а также получать цепные индексы из базисных и наоборот.
Для индексов с переменными весами такое правило не сохраняется.
С постоянными весами рассчитываются индексы физического объема продукции, а с переменными весами – индексы цен, себестоимости, производительности труда.
Индекс дефлятора используется для перевода значений стоимостных показателей за отчетный период в стоимостные измерители базисного периода.
Индекс дефлятора ВВП в 1998 г.
Для построения индекса дефлятора можно использовать индексы с переменными весами.
Индексы постоянного состава, переменного состава и структурных сдвигов В тех случаях, когда мы анализируем изменение во времени сравниваемой продукции, мы можем поставить вопрос о том, как в различных условиях (на различных участках) меняются составляющие индекса (цена, физический объем, структура производства или реализации отдельных видов продукции) . В связи с этим строятся индексы постоянного состава, переменного состава, структурных сдвигов.
Индекс постоянного (фиксированного) состава по своей форме тождественен агрегатному индексу.
|
Объединение |
Базисный |
Отчетный |
||
|
p 0 |
q 0 |
p 0 |
q 0 |
|
|
1 |
15 |
5000 |
11 |
20000 |
|
2 |
18 |
10000 |
13 |
15000 |
Цена по обоим предприятиям изменилась на 27,2 %.
Этот индекс не учитывает изменение объема продажи продукции на различных рынках в текущем и базисном периодах.
Индекс переменного состава используется для характеристики изменения средней цены в текущем и базисном периодах.
Цены снизились на 30 %.
Индекс структурных сдвигов
Индексы Пааше, Ласпейреса и "идеальный индекс" Фишера
Сводный индекс цены с базисными весами – это индекс цены Ласпейреса.
Надо отметить, что сводный индекс физического объема с базисными весами также именуется индексом физического объема Ласпейреса.
Сводный индекс физического объема с текущими весами – это индекс цены Пааше.
Аналогично сводный индекс цены с текущими весами также называется индексом цены Пааше.
Компромиссом явился "идеальный индекс" Фишера: Аналогичный индекс можно построить и для индексов физического объема.
Территориальные индексы
В статистике существует необходимость сопоставления уровней экономических явлений в пространстве. Для расчета значений используются территориальные индексы. Для их исчисления соответствующие показатели по всем видам продукции умножаются на количество продукции, произведенной во всей области.
Так как количество продукции каждого вида равно сумме продукции каждого вида в районе А и в районе В, расчет производится по формуле:
Индексы планового задания и выполнения плана Ряды динамики Задачи статистики в области рядов динамики
Понятие и виды рядов динамики
Ряд динамики – это ряд последовательно расположенных статистических показателей (в хронологическом порядке) , изменение которых показывает ход развития изучаемого явления.
Ряд динамики состоит из двух элементов: момента (периода) времени и соответствующего ему статистического показателя, который называется уровнем ряда. Уровень ряда характеризует размер явления по состоянию на указанный в нем момент (период) времени. В связи со сказанным различают моментные и интервальные ряды динамики.
В зависимости от способов выражения уровней различают ряды динамики, заданные: а) рядом абсолютных величин; б) рядом относительных величин; в) рядом средних величин.
Несопоставимость уровней рядов динамики
Уровни рядов динамики должны быть сопоставимы между собой. Для несопоставимых величин нельзя вести расчеты показателей рядов динамики.
Несопоставимость может быть:
Смыкание рядов динамики
В большинстве случаев уровни ряда приводятся к сопоставимому уровню путем пересчета. Например, может использоваться метод смыкания.
|
Продукция |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
|
22-х предприятий |
120 |
125 |
130 |
140 |
|
|
|
27-и предприятий |
|
|
|
170 |
175 |
192 |
|
Выровненный ряд |
80,0 |
82,2 |
86,7 |
100,0 |
102,5 |
112,9 |
Суть метода заключается в том, что уровень 1994 г. принимается за 100 %, а затем производим соответствующий пересчет. Получаем ряд относительных величин.
Показатели изменения уровней ряда
Характеристика показателей изменения уровней ряда достигается путем сравнения уровней ряда между собой.
Здесь различаются базисный и текущий периоды и т.п.
Большой проблемой является выбор базы сравнения. Этот выбор должен быть обусловлен теоретически. База сравнения – это наиболее характерный период в развитии изучаемого социально-экономического явления.
1. Абсолютный прирост Характеризует размер увеличения (уменьшения) уровней ряда за отдельный промежуток времени. Абсолютные приросты могут быть цепными или базисными.
Цепной: Базисный: 2. Темп роста Показывает, во сколько раз данный уровень ряда больше или меньше базисного уровня. Представляет собой соотношение двух сравниваемых уровней.
Цепной: Базисный: Темпы роста выражаются либо в виде процентов, либо в виде коэффициентов. Если темп роста больше единицы (100%) , то уровень ряда возрастает, если меньше – то убывает.
3. Темп прироста Показывает, на какую долю (процент) уровень данного периода или момента времени больше или меньше базового уровня. Темп прироста может быть измерен и как отношение абсолютного прироста к базовому уровню.
4. Абсолютное значение одного процента прироста Сравнение абсолютного прироста и темпа прироста за одни и те же промежутки времени показывает, что замедление прироста часто не сопровождается уменьшением абсолютных приростов. При замедлении темпов роста абсолютный прирост может увеличиваться, и наоборот.
Средние характеристики ряда динамики
Записанные характеристики ряда динамики относятся к каждому члену динамического ряда. Только базисные характеристики относятся ко всему периоду. Средние же характеристики полностью охватывают изменения за весь период, к которому относится динамический ряд.
1. Средний уровень ряда.
Показывает, какова средняя величина уровня, характерного для всего периода. Имеет смысл рассчитывать, когда величина изменения ряда более или менее стабильна.
Средний уровень ряда исчисляется по средней хронологической. Ее расчет для интервального и моментного ряда имеет свои особенности. Для интервального ряда, уровни которого можно суммировать, можно исчислять по средней арифметической простой.
Для моментного ряда с равноотстоящими уровнями: Для моментного ряда с неравноотстоящими интервалами: Например, даны следующие данные: 01.01.98 – 455 01.07 – 465 01.11 – 495 01.01.99 – 505 01.05 – 465 01.10 – 485 01.12 – 505 2. Средний абсолютный прирост Показывает скорость развития явления в изучаемом динамическом ряду. Он получается из абсолютных приростов как их средняя арифметическая. Может быть получен также как отношение абсолютного прироста за весь период к числу уровней без одного.
3. Средний темп роста Изменение (рост) социально-экономических явлений происходит по правилу сложных процентов. Средняя геометрическая из годовых темпов роста равна: 4. Средний темп прироста Выявление основной тенденции развития динамических рядов Существует два подхода: механическое и аналитическое выравнивание.
Механическое выравнивание:
Рассмотрим подробнее последний метод. Итак, смысл аналитического выравнивания методом скользящей средней состоит в том, что он позволяет сглаживать случайные колебания в уровнях развития явления во времени. Поэтому период охватываемой средней постоянно меняется.
Период осреднения как правило выбирается равным временному периоду, в течение которого начинается и заканчивается цикл развития какого-либо явления.
Пример расчета пятилетней скользящей средней:
|
Год |
у |
Скользящая средняя |
|
1990 |
10,9 |
– |
|
91 |
9,7 |
– |
|
92 |
13,1 |
11,40 |
|
93 |
11,1 |
11,98 |
|
94 |
12,2 |
12,78 |
|
95 |
13,8 |
12,82 |
|
96 |
13,7 |
13,26 |
|
97 |
13,3 |
13,24 |
|
98 |
12,8 |
– |
|
99 |
12,6 |
– |
У этого метода есть ряд недостатков:
Из-за этого не представляется возможным осуществлять прогнозирование развития изучаемых явлений.
Скользящая средняя может быть рассчитана и как взвешенная.
Методы аналитического выравнивания Это наиболее эффективные методы выравнивания. Имеют конечный вид функции времени (уравнения времени) . Возможно выравнивание по прямой, по гиперболе, по параболе 2-го или 3-го порядка.
Задача состоит в том, чтобы подобрать для конкретного ряда динамики такую логарифмическую кривую, которая бы наиболее точно отображала черты фактической динамики. Решение этой задачи часто связано с методом наименьших квадратов, т.к. наилучшим считается такое приближение выровненных данных к эмпирическим, при которых сумма квадратов их отклонений является минимальной: Техника аналитического выравнивания по прямой имеет наиболее простое выражение.
Система уравнений упрощается, если значение подобрать таким образом, чтобы т.е. перенести начало отсчета в середину рассматриваемого периода.
|
Годы |
Cтудентов |
t |
t 2 |
yt |
y t |
|
1986 |
98,4 |
-4 |
16 |
-393,6 |
94,8 |
|
87 |
97,9 |
-3 |
9 |
-293,7 |
96,0 |
|
88 |
97,2 |
-2 |
4 |
-194,7 |
97,2 |
|
89 |
95,7 |
-1 |
1 |
-95,7 |
98,4 |
|
90 |
95,0 |
0 |
0 |
0 |
99,6 |
|
91 |
99,2 |
1 |
1 |
99,2 |
100,6 |
|
92 |
102,4 |
2 |
4 |
204,8 |
102,0 |
|
93 |
104,0 |
3 |
9 |
312,0 |
103,2 |
|
94 |
106,2 |
4 |
16 |
424,8 |
104,4 |
|
|
896,0 |
0 |
60 |
73,4 |
896,4 |
Прогнозирование и интерполяция Прогнозирование (экстраполяция) – это определение будущих размеров экономического явления.
Интерполяция – это определение недостающих показателей уровней ряда.
Наиболее простым методом прогнозирования является расчет средних характеристик роста (средний абсолютный прирост, средний темп роста и т.д.) и перенесение их на будущие даты. Прогнозирование на основе аналитического выравнивания является наиболее распространенным методом.
Статистическое измерение связи
Задачи статистики в изучении связи. Взаимосвязанные признаки и их классификация.
Задачи статистики состоят в выявлении связи, определении ее направления и ее измерении. Наиболее же общая задача – это прогнозирование и регулирование социально-экономических явлений на основе полученных представлений о связях между явлениями.
Статистика рассматривает экономический закон как существенную и устойчивую связь между определенными явлениями и процессами. Познавая связи, статистика познает законы. А их знание позволяет управлять общественным развитием. Основой изучения связей является качественный анализ.
Различают два вида признаков:
Виды и формы связей, различаемые в статистике.
В статистике связи классифицируются по степени их тесноты. Исходя из этого различают функциональную (полную) и статистическую (неполную, корреляционную) связь.
Функциональная связь – такая связь, при которой значение результативного признака целиком определяется значением факторного (например, площадь круга) . Она полностью сохраняет свою силу и проявляется во всех случаях наблюдения и для всех единиц наблюдения. Каждому значению факторного признака соответствует одно или несколько определенных значений результативного признака.
Для корреляционной связи характерно то, что одному и тому же значению факторного признака может соответствовать сколько угодно различных значений результативного признака. Здесь связь проявляется лишь при достаточно большом количестве наблюдений и лишь в форме средней величины.
По направлению изменений факторного и результативного признака различают связь прямую и обратную.
Прямая связь – такая связь, при которой с изменением значений факторного признака в одну сторону, в ту же сторону меняется и результативный признак.
Обратная связь – такая связь, при которой с увеличением (уменьшением) факторного признака происходит уменьшение (увеличение) результативного признака.
По аналитическому выражению выделяются две основные формы связи:
Методы изучения связей
Описательные (механические) методы
К ним относятся: (1) метод приведения параллельных рядов,
(2) балансовый метод,
(3) графический метод,
(4) метод аналитической группировки.
Наибольший эффект достигается при комбинировании нескольких методов.
(1) Метод приведения параллельных рядов
Приводится ряд данных по одному признаку и параллельно с ним – по другому признаку, связь с которым предполагается. По вариации признака в первом и втором ряду судят о наличии связи признаков. Такой метод позволяет вывести только направление связи, но не измерить ее.
(2) Балансовый метод
Взаимосвязь может быть также охарактеризована с помощью балансов.
Пример: межрайонная связь.
|
Р-н приб. Р-н отпр. |
А |
Б |
В |
Г |
Итого отправлено |
|
А |
20 |
100 |
80 |
60 |
260 |
|
Б |
50 |
30 |
40 |
70 |
190 |
|
В |
40 |
60 |
25 |
80 |
205 |
|
Г |
100 |
50 |
90 |
35 |
275 |
|
Итого прибыло |
210 |
240 |
235 |
245 |
930 |
(3) Графический метод
Может использоваться как самостоятельно, так и совместно с другими методами.
Если конкретные данные перенести на график, то полученное изображение называется полем корреляции. На оси абсцисс откладывается значение факторного признака, а на оси ординат – результативного. Каждая единица, обладающая определенным значением факторного и результативного признака, обозначается точкой.
Беспорядочное расположение говорит об отсутствии связи. Наоборот, чем сильнее связь, тем теснее точки группируются вокруг определенной линии.
(4) Метод аналитической группировки
Сначала выбираются два признака: факторный и результативный. По факторному признаку производится группировка, а по результативному – подсчет средних или относительных величин.
Путем сопоставления характера изменений значений факторного и результативного признака можно сделать вывод о наличии связи и ее направлении. При помощи метода аналитической группировки можно сделать вывод и о тесноте связи.
Пример: среднегодовая з/п работников-текстильщиков в 1849 г.
|
Группы предприятий по числу работников |
З/п в рублях |
|
более 1000 |
219 |
|
501– 1000 |
204 |
|
101 – 500 |
198 |
|
51 – 100 |
188 |
|
24 – 50 |
192 |
|
менее 20 |
164 |
Аналитические методы
Это основные методы изучения связи. Они делятся на непараметрические и параметрические.
Непараметрические
Их еще называют ранговыми методами. Они связаны с расчетами различных коэффициентов. Применяются как отдельно, так и совместно с параметрическими. Особенно эффективны непараметрические методы, когда необходимо измерить связь между качественными признаками. Они проще в вычислении и не требуют никаких предположений о законе распределения исходных статистических данных, т.к. при их расчете оперируют не самими значениями признаков, а их рангами, частотами, знаками и т.д.
Коэффициент Фехнера (коэффициент совпадения знаков)
|
x |
y |
|
|
x 1 x 2 x 3 . . . x n |
y 1 y 2 y 3 . . . y n |
|
|
х = х i - х |
y = y i - y |
|
|
– + + – + + – |
+ + – – + – + |
|
Расчет основан на применении первых степеней отклонений значений признака от среднего уровня ряда двух связанных признаков.
|
i = |
кол-во совпадений – кол-во несовпадений |
|
общее количество отклонений |
|
i = |
3 – 4 |
= – |
1 |
|
7 |
7 |
Коэффициент совпадения знаков может принимать значения от –1 до +1. Чем ближе значение коэффициента к |1|, тем связь более тесная. Знак коэффициента говорит о направлении, величина – о силе связи.
Коэффициенты ассоциации и контингенции Используются для измерения связи между двумя качественными признаками, состоящими только из двух групп.
|
|
..... |
..... |
Итого |
||
|
..... |
a |
b |
a + b |
||
|
..... |
d |
c |
c + d |
||
|
Итого |
a + c |
b + d |
a + b+ c+ d |
||
|
Оценка Посещение |
Неудовлетв. |
Положит. |
Итого |
||
|
Посещали |
86 |
14 |
100 |
||
|
Не посещали |
22 |
28 |
50 |
||
|
Итого |
108 |
42 |
150 |
||
![]() – коэфф. ассоциации;
– коэфф. ассоциации;
![]() – коэфф. контингенции.
– коэфф. контингенции.
Коэффициент контингенции всегда меньше коэффициента ассоциации. Связь считается подтвержденной, если
![]() или
или
![]() .
.
Коэффициент Спирмана (ранговый коэффициент) Рассчитывается по следующей формуле:
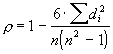 .
.
|
№ п/п |
Себестоимость единицы прод. |
Средняя з/п |
Ранги |
d i = R z - R f |
d i 2 |
|
|
R z |
R f |
|||||
|
1. |
68,8 |
168,5 |
3 |
6 |
-3 |
9 |
|
2. |
70,2 |
158,7 |
5 |
1 |
4 |
16 |
|
3. |
71,4 |
171,7 |
7 |
8 |
-1 |
1 |
|
4. |
78,5 |
183,9 |
10 |
10 |
0 |
0 |
|
5. |
66,9 |
160,4 |
2 |
2 |
0 |
0 |
|
6. |
69,7 |
165,2 |
4 |
5 |
-1 |
1 |
|
7. |
72,3 |
175,0 |
8 |
9 |
-1 |
1 |
|
8. |
77,5 |
170,4 |
9 |
7 |
2 |
4 |
|
9. |
65,2 |
162,7 |
1 |
3 |
-2 |
4 |
|
10. |
70,7 |
163,0 |
6 |
4 |
2 |
4 |
|
Итого |
|
|
|
|
|
40 |
Коэффициент Спирмана может принимать значения от –1 до +1, причем чем ближе значение коэффициента к |1|, тем связь более тесная. Знак коэффициента говорит о направлении связи.
Непараметрические Главным параметрическим методом является корреляционный. Он заключается в нахождении уравнения связи, в котором результативный признак зависит только от интересующего нас фактора (или нескольких факторов) . Все прочие факторы, также влияющие на результат, принимаются за постоянные средние.
Удобной формой изучения связи является корреляционная таблица. В этой таблице одни признаки располагаются по строкам, а другие – в колонках. Числа, стоящие на пересечении строк и колонок, показывают, сколько раз встречается данное значение факторного признака с данным значением результативного.
Рассмотрим следующую схему:
|
К-во станков Час. прод. |
3-5 |
5-7 |
7-9 |
9-11 |
f y |
|
10-15 |
5 |
|
|
|
5 |
|
15-20 |
2 |
4 |
2 |
|
8 |
|
20-25 |
|
6 |
1 |
|
7 |
|
25-30 |
|
|
6 |
|
6 |
|
30-35 |
|
|
2 |
2 |
4 |
|
f x |
7 |
10 |
11 |
2 |
30 |
По такой таблице можно сделать выводы (1) о том, существует ли связь, (2) о ее направлении и (3) о ее интенсивности (при условии существования связи) .
В указанных уравнениях величина результативного признака представляет собой функцию только одного фактора х. Все прочие факторы приняты за постоянную и выражены параметром а 0 .
Таким образом, при выравнивании фактические значения у заменяются значениями, вычисленными по уравнению. Поскольку все факторы, определяющие у, являются постоянными средними величинами, постольку и выровненные значения (у
х
) являются средними величинами (
![]() ) .
) .
Параметры а 1 (а в уравнении параболы и а 2 ) называются коэффициентами регрессии. В корреляционном анализе эти параметры показывают меру, в которой изменяется у при изменении х на одну единицу.
При линейной зависимости коэффициент регрессии а 1 называется также коэффициентом пропорциональности. Он положителен при прямой зависимости, отрицателен – при обратной.
Параметр же а 0 показывает влияние на результативный фактор множества неучтенных факторов.
Уравнение регрессии имеет большую ценность, поскольку позволяют экстраполировать показатели связи за пределы исследованных данных.
Корреляционное отношение для выровненных значений результативного признака рассчитывается так же, как и для значений, полученных на основе группировок.
В этом случае вся вариация результативного признака за счет всех факторов обозначается Вариация результативного признака за счет всех факторов, кроме х, равна Вариация за счет интересующего нас фактора х равна разности Дисперсия, характеризующая величину вариации за счет фактора х, может быть рассчитана непосредственно как Отсюда Данное корреляционное отношение применяется во всех случаях изучения связи для оценки ее тесноты независимо от формы связи (прямолинейной или криволинейной) .
Для прямолинейной связи может быть преобразовано в специальный линейный коэффициент корреляции Значение его колеблется от –1 до +1. Знак говорит о направлении, а величина – о тесноте связи.
Выборочный метод Основы выборочного метода Выборочное наблюдение – одно из наиболее современных видов статистического наблюдения. Выборочное наблюдение – это такое наблюдение, при котором обследованию подвергается часть единиц изучаемой совокупности, отобранных на основе научно разработанных принципов, обеспечивающих получение достаточного количества достоверных данных, для того чтобы охарактеризовать всю совокупность в целом.
Средние и относительные показатели, полученные на основе выборочных данных, должны достаточно полно воспроизводить или репрезентатировать соответствующие показатели совокупности в целом.
Логика выборочного наблюдения
Основные преимущества
Основные недостатки
Вся совокупность единиц, из которых производится отбор, называется генеральной. Совокупность единиц отобранных называется выборочной.
Для генеральной совокупности – Для выборочной совокупности – Обычно частота обозначается как, а относительная численность единиц выборочной совокупности, обладающая данным признаком, называется частостью –. Если численность единиц выборочной совокупности обозначить через, то получим: Ошибки выборки Чтобы оценить степень точности выборочного наблюдения, необходимо оценить величину ошибок, которые могут возникнуть в процессе проведения выборочного наблюдения.
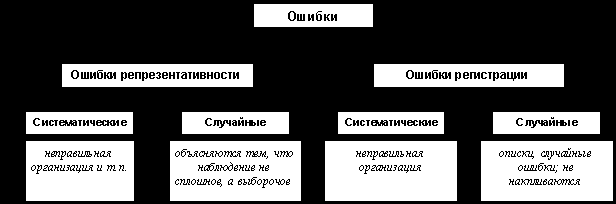
Основное внимание уделяется случайным ошибкам репрезентативности.
Средняя ошибка выборки Мерой колеблемости возможных значений выборочной средней является средний квадрат отклонений вариантов выборочной средней от генеральной, взвешенной по их вероятностям, т.е. дисперсия выборочной средней.
Отсюда видно, что средняя ошибка выборки прямо пропорциональна среднему квадратическому отклонению и обратно пропорциональна квадратному корню из численности выборки.
Если выборка используется для определения доли признака, то средняя ошибка выборки определяется по следующей формуле: Когда значение и значение неизвестны, то значение принимается равным.
Предельная ошибка выборки Средняя ошибка выборки используется для определения возможных отклонений показателей выборочной совокупности от соответствующих показателей генеральной совокупности.
С определенной вероятностью можно утверждать, что эти отклонения не превысят заданной величины, которая называется предельной ошибкой выборки.
Предельная ошибка связана со следующим равенством: – коэффициент, зависящий от вероятности, с которой можно гарантировать определенные размеры предельной ошибки выборки. Применительно к выборочному методу из теоремы Черышева следует, что с увеличением значений величина вероятности быстро приближается к единице.
|
t |
p |
|
1 |
0,683 |
|
2 |
0,954 |
|
3 |
0,997 |
|
4 |
0,999936 |
|
: |
: |
В связи с этим, увеличивая численность выборки, можно отклонение выборочной средней от генеральной довести до сколь угодно малых размеров, причем этот результат можно гарантировать с вероятностью сколь угодно близкой к единице.
Основные виды выборки, способы отбора Какой бы способ отбора мы не применяли, на последнем этапе в любом случае надо обеспечить случайную выборку, для того чтобы уменьшить размер выборки. Вид выборки определятся способом отбора единиц, подвергающихся наблюдению.
Выборочная совокупность может быть образована либо путем последовательного отбора единиц, либо путем последовательного отбора групп.
Если перед отбором совокупность разбивается на отдельные группы, из которых затем производится индивидуальный отбор, то такая выборка называется типической, районированной, стратифицированной. Если отбирают целые серии и в них проводится сплошное наблюдение, то такая выборка называется серийной, или гнездовой.
Выборка в любом из указанных видов может быть осуществлена путем повторного или бесповторного отбора. Повторный – это такой отбор, при котором каждая единица или серия участвует в отборе столько раз, сколько отбирают единиц или серий. При бесповторном отборе отобранная единица больше не участвует в отборе.
Случайность отбора обеспечивается следующими механизмами:
В зависимости от процедуры отбора расчет предельной ошибки выборки имеет определенную модификацию.
|
|
Предельная ошибка выборки |
|
|
Для средней |
Для доли |
|
|
Повторный отбор |
|
|
|
Бесповторный отбор |
|
|
Примеры задач
Пример 1. Найти среднюю и с вероятностью 0,954 – предельную ошибку среднего бала, если дисперсия успеваемости равна 0,56, а обследованию подвергнуто 100 студентов.
Что произойдет с ошибкой среднего балла, если обследовать 400 студентов? – Ошибка уменьшится в два раза. Это значит, что ошибку 0,06 можно будет гарантировать с вероятностью 0,954.
Пример 2.
Какую ошибку доли отобранных деталей можно ожидать с вероятностью 0,9, если дисперсия равна 0,09, а обследованию подвергнуто 400 деталей?
Численность выборки
Из формулы предельной ошибки выборки формула для расчета численности выборки: Пример 3. Сколько изделий необходимо отобрать для исчисления процента бракованных с ошибкой не более
![]() 2 % при вероятности 0,954, если вариация изучаемого признака максимальная.
2 % при вероятности 0,954, если вариация изучаемого признака максимальная.
Пример 4.
Какое количество станков надо обследовать, чтобы ошибка среднего срока службы не превышала 1 год с вероятностью 0,997, если дисперсия срока службы станка равна 25 годам.
Повторный групповой отбор
В зависимости от того, отбираются ли единицы или же группы, различают индивидуальный или групповой отбор. При повторном групповом отборе (повторный индивидуальный мы уже рассмотрели) предельная ошибка выборки равна:
|
Для средней |
Для доли |
|
|
|
|
|
|
Пример 5.
По данным выборочного обследования средняя удойность коров на 400 обследованных фермах составила 2200 литров в год. Найти ошибку удойности с вероятностью 0,954, если коэффициент вариации удойности коров между фермами равен 10 %.
Пример 6.
Сколько учебных групп необходимо обследовать, чтобы ошибка среднего балла успеваемости по интересующей нас дисциплине не превышала 0,2 с вероятностью 0,954, если дисперсия оценок между группами равна 0,1.
Многоступенчатый отбор
Ошибка многоступенчатого отбора в общем виде может быть представлена следующей формулой: Для комбинационного отбора предельная ошибка выборки равна: Пример 7. В результате комбинационной выборки оказалось, что средний процент выполнения норм выработки равен 135 %. Дисперсия признака между предприятиями равна 60, а в среднем для отдельных предприятий – 400. Рассчитать ошибку среднего процента выполнения норм с вероятностью 0,954, если на первой ступени отобрано 100 предприятий, а на второй – 1000 рабочих данной профессии.
Бесповторный отбор
При бесповторном отборе в формулу вносим коэффициент: Соответствующим образом модифицируем формулу для численности (при бесповторном отборе) : Определение границ изменения генеральной средней Пример 8. В результате выборочного наблюдения затраты времени на оформление финансовых документов мы поместили в таблицу.
|
Затраты времени |
20-22 |
22-24 |
24-26 |
26-28 |
Всего |
|
Число обследований |
67 |
133 |
127 |
73 |
400 |
Определить границы затрат времени на оформление финансовых документов с вероятностью 0,997.
|
Интервал |
|
|
|
|
|
|
20-22 |
21 |
67 |
-2 |
-134 |
268 |
|
22-24 |
23 |
133 |
-1 |
-133 |
133 |
|
24-26 |
25 |
127 |
0 |
0 |
0 |
|
26-28 |
27 |
73 |
1 |
73 |
73 |
|
Сумма |
|
400 |
|
-194 |
474 |
Таким образом, с вероятностью 0,997 можно утверждать, что время, затраченное на оформление одного финансового документа, равно